Using the Slavonic Abacus in the Classroom

The theory

There is increasing evidence to show that, although most teaching is based on words and depends heavily on spoken and printed language, this may not be the best way to work with some of our pupils. These are the 'spatial thinkers' in our classrooms, for whom thought is composed primarily of mental images. They can grasp complex sets of ideas, and see the connections between structures in a range of different contexts, but they cannot pick up information serially, as it is presented on the printed page.

For example, a linguistic thinker might give a set of directions in words:

'Turn right out of here, go to the T-junction at the end of this road and turn left. Then take the next left. The house you want is on the same pavement, opposite the lamp post.'

For a spatial thinker, on the other hand, the image might be a single overall gestalt, something like this:

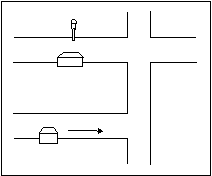
The serial processing of the linguistic thinker matches the way that ideas are presented on the printed page. The spatial thinker, on the other hand, is better able to 'see' the whole – often quite literally, as a sort of mental model or diagram – but may be less able to transfer this understanding into a linear, written account.

But teachers rely heavily upon linguistic assessments, formal and informal, as indicators of their pupils' intellectual potential. Children with poor linguistic ability who exhibit signs of good spatial ability are damned with faint praise. Tommy is 'slow, but with an artistic gift'. Jenny is 'good with her hands, but not very bright'. But how often is a child described as 'slow, but with a linguistic gift', or 'a good talker, but not very bright'? Linguistic ability is valued: spatial ability is devalued in our classrooms.

Numeracy for spatial thinkers

The heavy reliance on the printed page affects the whole of the school curriculum, but it is perhaps particularly pernicious in its effects on mathematics education. Mathematics is a subject in which one feels that spatial thinkers ought to do well: but, at least at school, they often fail. They seem unable to 'remember' anything from one day to the next. For the teacher the situation is puzzling and frustrating: for the pupil, who may become convinced that she is just ‘stupid’, it can be devastating.

Spatial thinkers may do well enough to at least pass muster in the parts of the mathematics curriculum dealing with shape and space, but they often have great difficulty with the all-important numeracy curriculum. They simply cannot remember number bonds or learn the multiplication tables.So how can the Slavonic abacus help?

Pictures in the mind: the Slavonic abacus

The secret in working with spatial thinkers is always to offer an image. This may well be a concrete image, at least to begin with – internalisation of the image, so that it becomes a mental picture or model which pupils can conjure up for themselves when they need it, comes later. The Slavonic abacus, described by Grauberg in her book Elementary Mathematics and Language Difficulties, provides an invaluable tool to enable pupils to 'see' numbers and number bonds to ten, and then to a hundred. This is just a common hundred-bead abacus. What makes it special is the colouring of the beads. Each row and column is divided into two sets of five beads.

With a little practice – and it may come almost automatically to the spatially oriented pupil – the eye can 'see' a row of up to four beads as a whole, and recognise, without counting, that

is 'three' or that

is 'four'.

Longer rows of beads are harder to distinguish – but that is where the special colouring of the Slavonic abacus comes in. Five beads can be distinguished readily from the rest of the row because they are all one colour.

But now the way is open for the pupil to just see (not to count: to see) six, seven, eight or nine beads. Eight, for example, is just a row of five (which can be seen at a glance), plus a row of three (which can also be seen at a glance).

Furthermore, a single row of the Slavonic abacus shows the complement to ten. The beads left over at the other end of the row also form a set which can be seen at a glance – so, for example, ten is eight plus two.

Once this model is internalised, numbers which add to ten can be seen in the mind's eye, as patterns of beads. These are far more meaningful, and therefore memorable, than the endless lists of number bonds to ten which the spatial thinker can never recall.

In the same way, pupils using the Slavonic abacus can learn to see two-digit numbers, and their complements to a hundred.

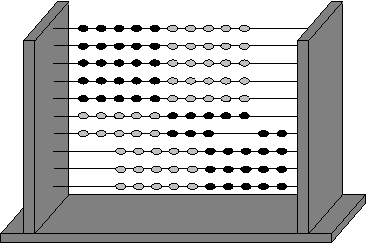
The 'sixty' of 'sixty-eight' can be seen as 'five-plus-one' rows of ten, while the 'eight' is 'five plus three' beads. The complement to a hundred falls immediately into place, as 'three' rows of ten, plus 'two' beads. There is nothing for the pupil to learn, only an image to create on the abacus, to understand, and to remember.

A model for multiplication

With the Slavonic abacus, pupils learn to recognise the numbers one to four,

and their column equivalents, without counting. This paves the way for the recognition of rectangular arrays up to four by four, without counting:

These arrays may be put onto square cards, and pupils may be taught to identify them. (See the end of these notes for a set of arrays which may be printed out and photocopied onto card.) By focusing on the spatial, rather than the symbolic, representations of the products, the inter-relationships between them are brought out clearly. For example, 'four fours' is composed of 'two lots of two fours' – the array is literally made up of two pairs of two rows of four beads.

Again, multiplication is commutative – it depends which way up you hold the card whether 'six' is seen as 'three twos' or 'two threes'.

Multiplying numbers over five

To multiply a pair of single digit numbers over five, the pupil can isolate a rectangle whose edge lengths are the numbers to be multiplied. For example, to multiply eight by seven, an eight by seven rectangle is needed.

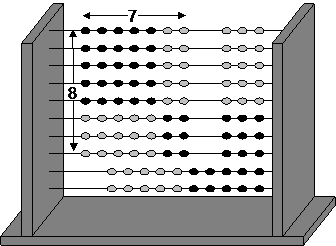
The Slavonic abacus enables pupils to see numbers over five as a row of five plus a number of ones. This skill enables them to identify the rectangle and slide the beads to one side without counting. Once the rectangle is isolated, the product may be read off the abacus.

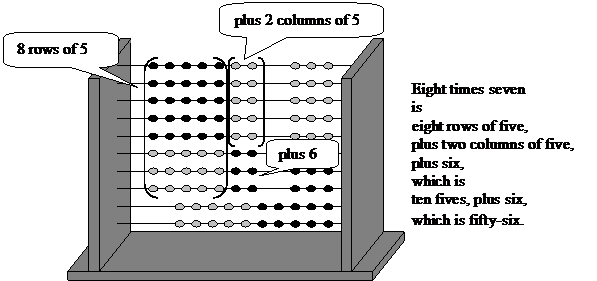
Pupils will need to practise using the abacus in order to build up a mental image of the arrangements of the beads. With time, however, they may learn to visualise the abacus, and use it flexibly to carry out the mental calculation to find the product of any pair of single digit numbers – that is, they may use it to work out the multiplication tables which they find it so hard to memorise.

Building the images

Finding ways to make mathematics meaningful for all our pupils is a constant challenge – but without meaning, our attempts to teach are pointless. Pupils who do not understand will not remember. For some pupils,

2 x 7 = 14

may be meaningful as it stands, and will do well enough. But for others – and particularly for those found in 'bottom sets' and in special schools – the squiggles on the page remain just that: meaningless squiggles. On the other hand, a concrete image of two rows of five-plus-two beads, which can be created on the Slavonic abacus and can eventually be recalled as a picture in the mind, provides a basis for real understanding to develop.

The two fives make ten, and the square array formed by the remaining dots is 'four'. These numbers can be seen and understood in a way that the written numbers '10' and '4' cannot.

Tandi Clausen-May’s book, Teaching Maths to Pupils with Different Learning Styles, offers many more ideas and activities to use in the classroom. By modelling abstract concepts, and making them meaningful, we can build on our pupils' strengths, and help them to learn.

References

Clausen-May, T. (2005) Teaching Maths to Pupils with Different Learning Styles. London: Paul Chapman Publishing. ISBN 1-41290-359-9

Grauberg, E. (1998). Elementary Mathematics and Language Difficulties. London: Whurr Publishers, ISBN 1-86156-048-6

Tandi Clausen-May, March 2005